Likelihood & Maximum Likelihood Estimation(MLE)
Likelihood(우도; 가능도)란? 어떤 모델(파라미터;확률분포)과 데이터가 주어졌을 때,
이 모델이 데이터를 얼마나 잘 설명하는지? 수치화 할 수 있는 척도이다.
Likelihood는 모델의 파라미터 θ에 대한 함수이다.
관측된 데이터가 주어졌을 때, 어떤 파라미터 θ가 입력되느냐에 따라
Likelihood 함수 결과값의 높고 낮음이 결정 된다.
예를 들어,
이항 분포의 확률 B(n, p)을 정의하는 확률 질량 함수가 있고
n번 동전을 던져 x번 앞면이 나올 확률은 다음과 같이 구할 수 있다하자.
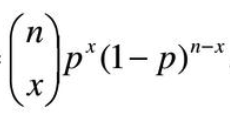
모델 파라미터 p를 모르는 상태에서
데이터를 관측한 결과 n=100, x=24가 나왔다면
이를 대입한 100C24 * p^24 * (1-p)^76 에 p 값을 넣어 얻은 값이 likelihood
이다.
참고로,
이산 확률 분포에서는 확률 값 == 가능도 이지만
연속 확률 분포에선 확률 밀도 값 == 가능도 이다.

n번의 독립 시행을 거쳐 얻은 데이터에 대한 우도는
모델에 관측된 데이터를 모두 넣어, 각각에 대한 확률을 뽑고
얻어낸 확률들을 모두 곱함으로써 얻을 수 있다.

그 수치가 높다면? 그 모델은 해당 데이터를 잘 표현/설명하는 것이라 할 수 있다.
(데이터의 확률분포를 잘 흉내내는 것)
그런데, 확률들이 곱해지다보면 underflow 현상이 일어날 수 있다.
이를 방지하기 위해 log를 취함으로써 곱을 합으로 바꿀 수 있다. (Log Likelihood)
* 가우시안 분포에서는 지수를 제거할 수 있는 이점
따라서, 어떤 확률분포를 흉내내는 모델을 만들고 싶다면
1. 흉내내고 싶은 데이터 분포에서 데이터를 샘플링하고
2. 랜덤 파라미터를 가지는 모델을 이용해 확률 분포 함수를 생성 후
(가우시안 분포를 가정한다면 파라미터로 랜덤한 평균, 표준편차 설정)
(뉴럴넷의 W들도 결국 임의의 확률분포를 표현하는 파라미터라 할 수 있음 ; 뉴럴넷 == 확률분포함수)
3. 주어진 모델과 데이터를 이용해 확률값들을 뽑아 Likelihood를 계산하고
4. 2-3 반복 후 Likelihood를 최대화하는 모델 선택
브론즈식으로 랜덤 초기화 + 데이터를 넣어보고 Likelihood를 구하길 무한 반복해서
Likelihood를 최대화 하는(Maximum Likelihood Estimation),
가장 적합한 파라미터를 찾을 수도 있겠지만
Gradient Ascending을 통해서 찾을 수도 있다는 거
이 때 최소화 문제로 변형해서 풀고 싶다면 앞에 마이너스를 붙이면 된다.
이게 바로 Negative Log Likelihood(NLL) 이고,
Gradient Descent 알고리즘을 통해 최적화가 가능해진다.
딥 뉴럴넷은
x ~ P(x) 가 주어졌을 때 (== 해결하고자 하는 문제의 Ground Truth 분포 P(x)에서 샘플링한 데이터 x)
조건부 확률 분포 P(y given x ; θ)를 나타낸다.
NLL을 최소화 하는 파라미터를 찾음으로써 최적화가 가능하다.
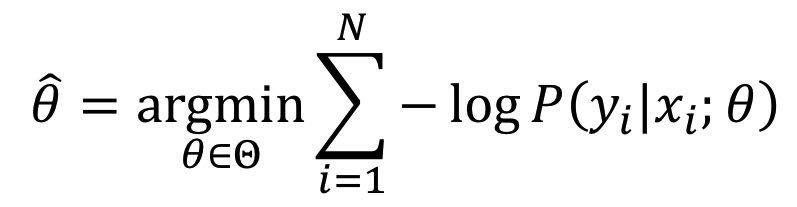
실제 구현할 때는 아래와 같이 변형하여 (의미적으로 동일)
아래 식을 argmin하는 파라미터를 찾으면 된다.

y_i는 정답을 표현한 원핫 벡터(ex. [0, 0, 0, 0, 1])
y_i_hat은 모델의 예측 확률 값을 담은 벡터(softmax 결과)
결과적으로 보면, MLE(NLL) 수식은 Cross Entropy Loss 수식과 매우 비슷하다.
Cross Entropy는 정보 이론 관점의 해석이라 할 수 있음.
추가 참고 자료
[수리통계학] 가능도는 확률과 어떻게 다르지? (가능도(Likelihood) VS. 확률(Probability))
통계학을 공부하다 보면, 무조건 만나게 되는 개념 중에 가능도(likelihood)라는 개념이 있다. 이 부분은 ...
blog.naver.com
[기초통계 정리 2] - Probability, Likelihood, MLE와 Python 구현
Deep Learning까지 가지 않더라도, 대부분의 머신 러닝의 개념에서는 확률과 우도의 개념이 빈번하게 등장한다. 그래서 기초 통계를 공부하던 도중, Probability와 Likelihood의 개념을 조금 더 자세하고
yamalab.tistory.com
Bayes Rule (베이즈 룰) | Hyeongmin Lee's Website
Bayes Rule은 Bayesian Deep Learning에서 가장 기본이 되는 개념입니다. 어떤 값을 예측하기 위한 수단으로서 딥러닝 이전부터 굉장히 많이 쓰여 왔던 방식이기 때문에 Bayesian Deep Learning이 아니더라도 알
hyeongminlee.github.io
Maximum Likelihood Estimation(MLE) & Maximum A Posterior(MAP) | Hyeongmin Lee's Website
Bayes Rule을 이용한 방식의 가장 큰 단점들 중 하나는 Likelihood의 Probability Distribution을 알아야 한다는 점입니다. 물론 앞선 포스팅에서는 관찰을 통해 Likelihood를 얻었지만, 여간 귀찮은 일이 아닐
hyeongminlee.github.io
'DL&ML > concept' 카테고리의 다른 글
| Under/overfit, Validation, Regularization, Dropout, Normalization, Ensemble etc. (0) | 2021.03.10 |
|---|---|
| Cross Entropy, KL-Divergence (0) | 2021.03.10 |
| MAP(Maximum A Posterior) (0) | 2021.03.10 |
| One-shot learning (siamese network) (0) | 2020.10.23 |
| Transformer (0) | 2020.10.21 |