Cross Entropy, KL-Divergence

 

두 확률 분포 사이의 다름의 정도를 측정하는 방법에 대해 정리해 본다.

Cross Entropy

Cross Entropy를 이해하기 앞서서 information에 대해서 정의해야 한다.

information(정보량)은 uncertainty(불확실성)을 나타내는 지표이며,

확률에 -log를 취한 것이다.

 

확률이 낮으면 값이 커지고, 높을 수록 값이 작아짐.

 

information에 대한 기대값(평균)이 바로 Entropy이며,

분포의 평균적인 불확실성을 표현하는 값이다.

 

Entropy가

높다면, 분포가 flat한 것이고 (어떤 지점에서든 헷갈리니까 ; 확률이 비슷비슷)

낮다면, 분포가 sharp한 것이다. (확률이 대부분 낮고, 특정 포인트가 높음 ; 확실하니까)

 

그러면, Cross Entropy란 뭐냐,

두 분포 P, Q가 있을 때,

P 관점에서 본 Q의 정보량의 평균으로 정의 된다.

(P에서 샘플링한 x를 통해 Q의 평균 정보량을 나타낸 것)

두 분포가 비슷할(가까울) 수록 작은 값을 가진다.

 

Cross Entropy

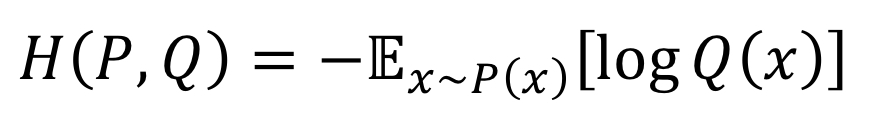
주로 분류 문제에서 정답 분포와 모델의 예측 분포를 비슷하게 맞출 때 활용된다.

 

몬테카를로 샘플링을 통한 식 변형

 

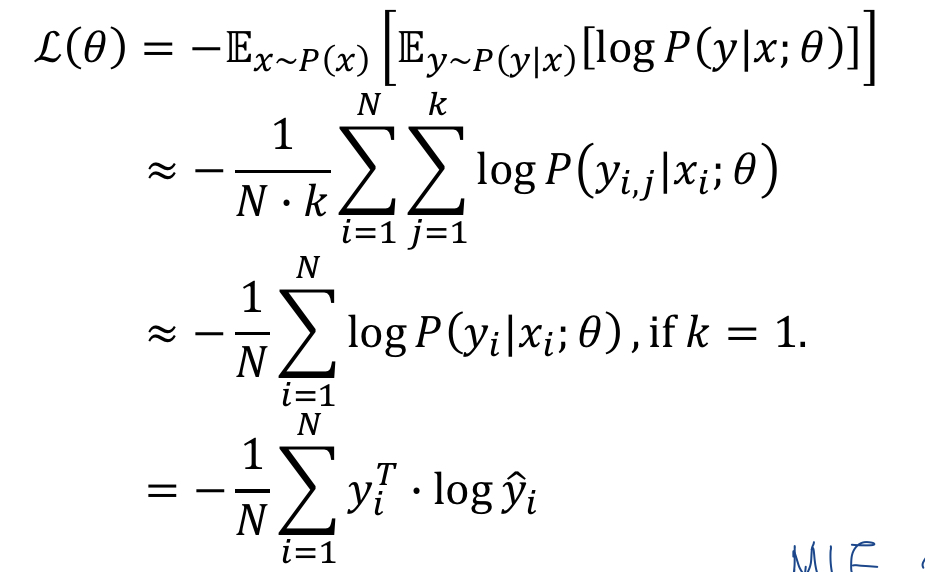
실제로는 위 그림의 마지막 식 같이 구현되며 (y, y_hat은 모두 벡터)

앞의 1/N텀을 빼면 MLE의 수식과 일치(NLL을 최소화 하는 식)한다.

* P(y|x;θ)는 확률 '분포'를 반환하는 함수, 클래스별 확률 값

 

같은 의미지만, 나에게 이해가 더 직관적으로 다가오는 형태는 이것...

 

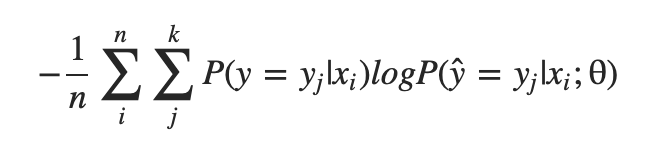
보통 우리가 분류 모델을 학습함에 있어

Loss를 구할 때 (기댓값을 구할 때)

그 샘플이 등장할 확률은 별도로 고려하여 weighted average를 구한 것이 아니라,

균등히 등장할 것이라는 가정으로 다 더해서 1/N을 해줬다.(몬테카를로 샘플링)

 

Kullback-Leibler Divergence

두 분포 P, Q가 있을 때,

P, Q 사이의 Disimilarity를 측정하는 방법이다.

 

P관점에서 Q의 다름의 정도를 측정

 

P, Q 의 순서를 바꾸어 측정했을 때는 값이 달라지므로 asymmetric한 특징을 가지고 있다.

따라서 Distance라고 볼 수 없다.

 

두 분포가 비슷할 수록 작은 값을 가지며,

완전히 일치할 때 0이 나온다.

 

아래 식 전개를 통해서 KL-divergence는 Cross entropy + Entropy의

조합으로 이루어 져있다는 사실 또한 알 수 있다.

 

KL divergence 식 분해

 

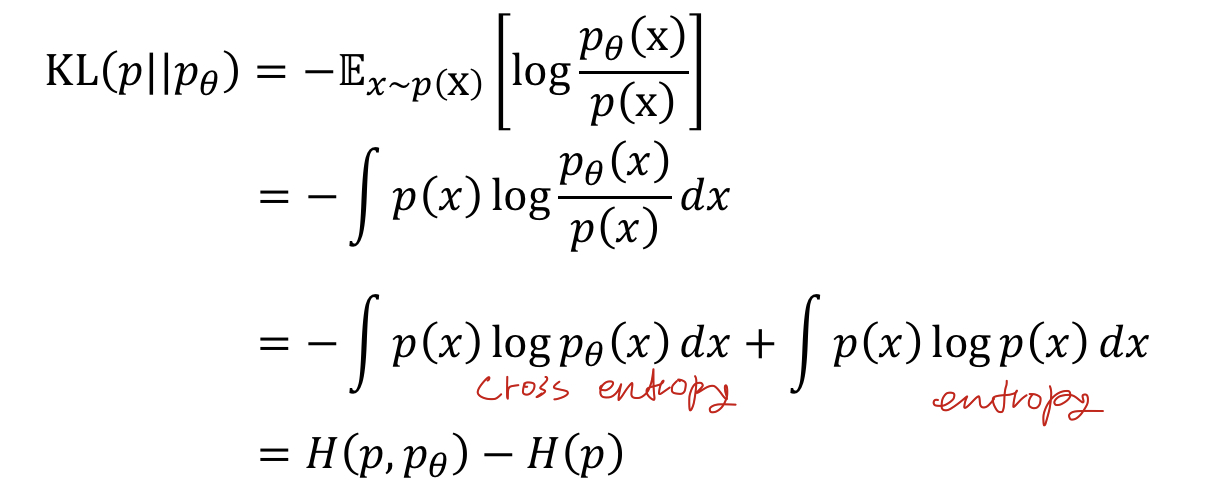
최적화시 파라미터에 대해서 미분할 경우 entropy 부분이 날아가서

결과적으로 cross entropy와 같은 수식에 대해서 최적화 한다고 볼 수 있다.