Density Estimation / Clustering / Anomaly Detection에 활용될 수 있는
Gaussian Mixture가 무엇인지 대략 살펴 보려 한다.
Gaussian Mixture
인스턴스(데이터)들이 파라미터가 알려지지 않은 몇 개의 가우시안 분포의 믹스쳐로 부터 생성이 되었다고 가정하는 확률 모델이다.
가정이 그렇기 때문에,
인스턴스(데이터) x가 주어지면 인스턴스 기반으로 가우시안 분포의 파라미터 등을 거꾸로 추정하고,
새로운 데이터가 확률적으로 어떤 가우시안 분포(클러스터)에 속하는지 여부를 알 수 있게 된다.
하나의 분포(multivariate gaussian distribution)로 부터 생성된 인스턴스들은 하나의 클러스터를 이루며,
모양에 제한은 없으나 보통은 타원 모양을 이룬다.
그리고, 각 클러스터는 파라미터에 따라 타원의 모양, 크기, 밀도(density), 그리고 방향이 제각기 달라지게 된다.

데이터가 몇 개(k개)의 클러스터로 구성되는지 사전에 알고 있다고 가정할 때,
데이터는 다음의 과정을 통해 생성 된다.
[1] 각 인스턴스(m개)를 k개의 클러스터 중 하나에 랜덤하게 배정한다.
j 번째 클러스터를 선택할 확률은 클러스터의 weight인 ϕ(mixing coefficient)에 의해 결정 된다.
i 번째 인스턴스에 매핑된 클러스터 인덱스는 z^(i) 로 표기 한다.
[2] i번째 인스턴스의 위치 x^(i)는 j 번째 클러스터의 가우시안 분포로 부터 랜덤하게 샘플링한다.
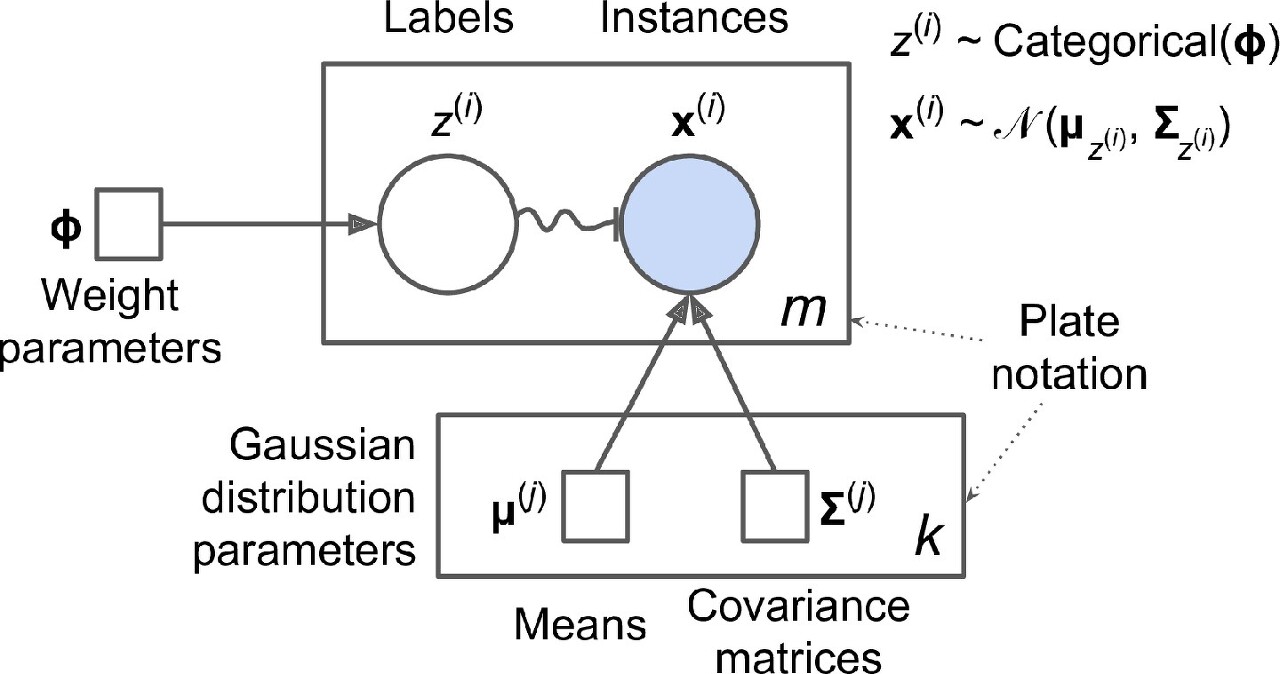
가우시안 믹스쳐 모델을 시각화 한 것이 위의 그림이다.
각 기호의 모양이 의미를 지니고 있는데,
정사각형은 parameter, 원은 random variable(vector), 화살표는 conditional dependency를 나타낸다.
직사각형은 포함 된 요소가 여러 번(오른쪽 아래 숫자) 반복 됨을 의미한다.
m개의 random vector ; x^(i)
k개의 평균 벡터와 공분산 행렬
참고로,ϕ는 1개의 벡터 (k개의 weight 포함)
다시 정리해서 말하면,
z^(i)는 ϕ파라미터를 갖는 categorical distribution에서 샘플링 된 것이고
x^(i)는 특정 클러스터( j )가 정의(μ; 평균, Σ; 공분산 행렬)하고 있는 normal distribution에서 샘플링 된 것이다.
마지막으로 구불거리는 화살표로 표현된 부분은 switch를 의미한다.
z^(i)는 i번째 인덱스에 배정된 클러스터의 인덱스인데,
그 값에 의해서 인스턴스의 위치 x^(i)가 샘플링 될 가우시안 분포가 결정되기 때문이다.
if z^(i) = j, then x^(i) ~ N(μ^(j), Σ^(j))
따라서 위와 같은 프로세스로 데이터가 생성 되었다고 가정 한다면,
알려진 인스턴스의 위치를 기반으로
각 클러스터를 표현하는 weight 및 gaussian distribution의 parameter를 학습할 수 있게 된다.
* scikit-learn의 GaussianMixture 클래스를 이용해서 쉽게 모델링 가능하다.

학습을 위해 x에 대한 likelihood를 정의 했을 때, 관측 가능한 random variable만 포함된 것이 아닌
임의로 설정된 hidden variable이라 할 수 있는ϕ(latent variable)가 포함되어 MLE로는 학습 할 수 없다고 한다.
MLE 대신에, Expectation-Maximization(EM) 라고 하는 알고리즘에 의해 반복적으로 진행 된다.
학습의 흐름은 대략 다음과 같다.
[Expectation step]
각 인스턴스에 대해서 각 클러스터에 속할 확률을 추측 (현재 클러스터의 파라미터는 고정)
[Maximization step]
각 클러스터를 모든 인스턴스를 이용해 업데이트 시킨다 (각 인스턴스가 각 클러스터에 속할 확률은 고정)
클러스터의 responsibility가 높은 인스턴스에 의해 영향을 많이 받게 됨.
*인스턴스가 각 클러스터에 속할 확률을 responsibility of the cluster for the instance라고 표현함
* todo ; 학습 과정에 대한 수식적인 이해가 더 필요하다..
Machine learning 스터디 (14) EM algorithm - README
들어가며 EM 알고리즘은 latent variable이 존재하는 probabilistic model의 maximum likelihood 혹은 maximum a posterior 문제를 풀기 위한 알고리즘 중 하나이다. 굉장히 많은 probabilistic 모델을 풀기 위해 널리 사용
sanghyukchun.github.io
기댓값 최대화 알고리즘
위키백과, 우리 모두의 백과사전. 올드페이스풀 간헐천 분화 데이터. 데이터가 정규분포 혼합 모델에서 관측되었다고 가정하고, 기댓값 최대화 클러스터 분석을 이용해 매개변수들을 추정하는
ko.wikipedia.org
가우시안 믹스쳐는
K-means의 일반화 버전이라고 볼 수 있음,
centroid(μ)를 찾을 뿐만 아니라, 크기, 모양, 방향 (Σ)
그리고 클러스터 간의 상대적인 가중치 (ϕ)까지 학습한다.
K-means와 차이점은 hard-assignment가 아닌 soft-assignment라는 것이다.
추가 참고자료
[머신 러닝/군집화] 가우시안 혼합 모델 (Gaussian Mixture Model, GMM)
Gaussian Mixture Model (GMM)은 이름 그대로 Gaussian 분포가 여러 개 혼합된 clustering 알고리즘이다. 현실에 존재하는 복잡한 형태의 확률 분포를 [그림 1]과 같이 $K$개의 Gaussian distribution을 혼합하여..
untitledtblog.tistory.com
머신러닝 - 수식 없이 이해하는 Gaussian Mixture Model (GMM)
수식없이 이해하는 Gaussian Mixture Model /* 2017.8.4 by. 3개월 */ 개요 머신러닝에서 자주 사용되는 Gaussian Mixture Model(GMM)을 알아보겠습니다. GMM은 머신러닝에서 Unsupervised Learning(클러스터링)에..
3months.tistory.com
'DL&ML > concept' 카테고리의 다른 글
| Optimizers (momentum, RMSProp, Adam, AdamW) (0) | 2021.04.11 |
|---|---|
| Seq2Seq, Auto Regressive, Attention, Teacher Forcing, Input Feeding (0) | 2021.04.07 |
| 비지도 학습 (Clustering ; K-means, DBSCAN, *Semi-supervised Learning, Active Learning) (0) | 2021.03.14 |
| 확률 관련 개념 (Random Variable, Covariance Matrix, Multivariate Gaussian) (0) | 2021.03.13 |
| Measure (Precision, Recall, F1-score, ROC, AUC) (0) | 2021.03.11 |