기본적인 옵티마이저들에 대해서 정리해 놓자.
아래와 같은 흐름으로 옵티마이저의 발전 흐름을 정리할 수 있다.

SGD
SGD는 미니배치에 대해 그래디언트를 구함으로써
학습이 빠르다는 장점이 있다.
배치를 다 보면 아무래도 메모리가 부족하고, 계산에 시간이 오래 걸리니...
그렇다고해서 수렴이 빠르다고 할 수는 없다.
SGD의 문제점
- 로컬 미니마를 벗어나기 힘들고 갖힐 경우 수렴이 느림
- 스텝사이즈가 모든 파라미터에 대해 똑같음 (상수 러닝레잇을 곱해줌)
어떤 weight은 많이 업데이트 되었고,
어떤 weight에 대해선 그렇지 않다면 각 weight 별로 스텝이 달라져야하지 않을까?
크게 두 가지 문제점을 해결하는 방향으로 옵티마이저가 발전해왔다.
Momentum
기울기의 움직임에 대해 관성을 부여해서 로컬 미니마를 벗어나기 위한 장치를 마련한 방법.
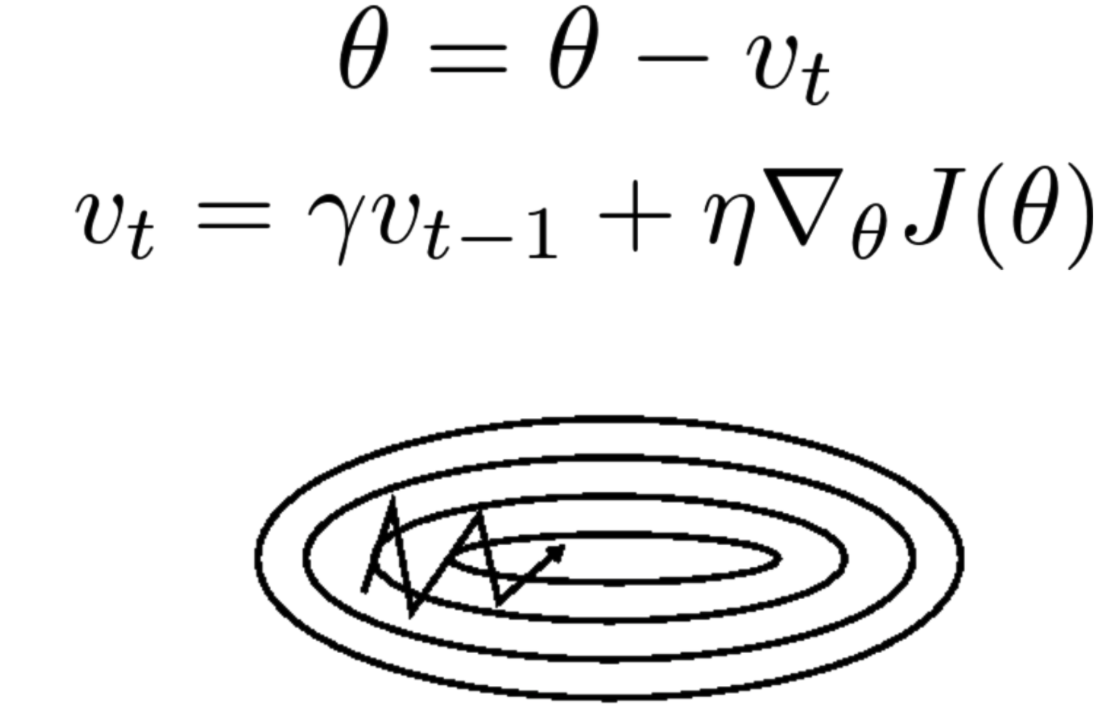
위와 같은 식을 통해 그래디언트가 업데이트 되며
- decay 상수 감마를 두어 누적 된 기울기를 얼마나 반영할 것인지 정도를 정함.
- SGD의 oscillating 문제를 해결한다. (시작점에 따라 미니멈 방향과 다른 방향으로 진동해버릴 수 있는 문제)
모멘텀의 문제점?
미니멈 근처에서 멈추기가 힘들다는 문제를 갖는다.
NAG (Nesterov Accelerated Gradient)
모멘텀의 문제를 해결하고자,
모멘텀과 그래디언트 합의 위치로 이동하는 것이 아닌
모멘텀을 반영하여 이동한 후, 그 위치에서 기울기를 구해 또 한번 이동한다.
즉, 현재 파라미터 기준으로 모멘텀 만큼 이동 한 후에, 기울기를 구한 후 이동하는 방식.

여기 까지 로컬 미니마를 벗어나기 위한 노력,
여기 부터는 러닝레잇의 스텝을 좀더 adaptive하게 가져가기 위한 노력.
AdaGrad
아다그래드는 그래디언트의 제곱을 더한 텀을 누적시켜가면서
누적 값을 이용해 러닝레잇을 보정해준다.
아래 식 기준으로는 G_t(파라미터 개수만큼의 길이 벡터라고 생각..)에
해당 파라미터에 대한 그래디언트 제곱을 누적시켜 추적한다.
G_t + 엡실론(0으로 나눠지는 것 방지 위한 작은 상수)으로 러닝레잇을 나눠줌으로써
변해온 만큼의 반비례 하는 정도로 스텝을 밟을 수 있게 해준다.

아다그래드의 문제점은
G가 마냥 무한히 커지기만 한다는 것.
따라서 특정 시점에 학습이 멈춰버릴 여지가 있다.
RMSProp
그걸 개선한 것이 RMSProp이다.
아다그래드와 비슷한데, 디케잉 상수를 도입해서 무한히 커지는 것을 방지한다.

이제 두 방향(로컬 미니마 탈출, adaptive한 스텝)의
장점을 통합한 방법을 살펴보자.
* Adam
모멘텀 + RMSProp의 장점을 취합해 놓은 것이 아담 옵티마이저이다.
아래 식에서
g_t는 그래디언트를 의미하며
m_t는 위에서 살펴봤던 모멘텀
v_t는 adaptive learning rate을 위한 텀을 의미한다.
일반적으로 beta_1=0.9, beta_2=0.999으로 초기화 된다.
m_t hat과 v_t hat은 학습 초반에 이전 누적값이 0이되면서 m_t는 매우 크고, v_t는 매우 작은 현상을 보정하는 작업이다.

* AdamW
L2 regularization 텀이 추가된 loss func를 Adam을 이용해서 최적화 할 경우, 의도와 달리 일반화 효과과 떨어질 수 있다고 한다.
(SGD에선 의도대로 weight decay의 효과를 가짐)
그 이유를 직관적으로 생각해 보면, Adam은 adaptive learning rate을 위해
그래디언트 제곱 누적 값의 역수에 루트를 취한 것으로 learning rate을 나눠 주기 때문에
L2 regularization 텀이 포함 된 loss func를 전개해 보았을 때,
SGD에 적용한 것 보다 보다 decay rate이 더 작아질 가능성이 있는 것을 확인할 수 있다.
자세한 수식 전개가 궁금하다면 아래 히든비기너(이동진)님 블로그를 참고하자.
[논문 리뷰]AdamW에 대해 알아보자! Decoupled weight decay regularization 논문 리뷰(1)
재야의 숨은 고수가 되고 싶은 초심자
hiddenbeginner.github.io
따라서 L2 regularization과 별도로 weight decay를 위한 텀을 수식에 추가하여 AdamW가 만들어졌다.

transformers의 AdamW 옵티마이저, weight_decay 파라미터를 통해 decoupled weight decay를 적용할 수 있다.
Optimization
The.optimization module provides: an optimizer with weight decay fixed that can be used to fine-tuned models, and, several schedules in the form of schedule ...
huggingface.co
참고자료
Gradient Descent Optimization Algorithms 정리
Neural network의 weight을 조절하는 과정에는 보통 ‘Gradient Descent’ 라는 방법을 사용한다. 이는 네트워크의 parameter들을 $\theta$라고 했을 때, 네트워크에서 내놓는 결과값과 실제 결과값 사이의 차이
shuuki4.github.io
꿀강의..
'DL&ML > concept' 카테고리의 다른 글
| Posterior, Likelihood, Prior (0) | 2021.04.12 |
|---|---|
| Regression에서 MSE를 Loss 함수로 쓰는 이유? (0) | 2021.04.11 |
| Seq2Seq, Auto Regressive, Attention, Teacher Forcing, Input Feeding (0) | 2021.04.07 |
| 비지도 학습 (Gaussian Mixture) (1) | 2021.03.15 |
| 비지도 학습 (Clustering ; K-means, DBSCAN, *Semi-supervised Learning, Active Learning) (0) | 2021.03.14 |