유사 이미지, 유사 텍스트를 찾는 태스크를 건들여보고 있는데,
이 때 입력을 잘 표현하는 임베딩을 학습하는 방법이 필요했다. (클러스터링에 활용할...)
arcface에 대해선 이전에 들어보기는 했지만, 실제로 어떻게 동작하는지도 잘 모르겠고
뭐, 대충 메트릭 러닝이라곤 들었는데, 메트릭 러닝이라고 하면 유일하게 들어 본 것이
triplet loss 정도...? 였다.
아는게 triplet loss이다 보니, arcface도 비슷하게 동작/구현 되지 않을까? 라는
편견에 사로 잡혀 코드를 이해하는데 한참 걸렸다.
아래 코드를 보면 알겠지만, triplet loss처럼 입력으로
여러 비교 대상(anchor, positive, negative)이 들어오지 않고
단일 입력(+정답 라벨)을 기대하기 때문이다.
코드 출처 (github.com/wujiyang/Face_Pytorch/blob/master/margin/ArcMarginProduct.py)
import math
import torch
from torch import nn
from torch.nn import Parameter
import torch.nn.functional as F
class ArcMarginProduct(nn.Module):
def __init__(self, in_feature=128, out_feature=10575, s=32.0, m=0.50, easy_margin=False):
super(ArcMarginProduct, self).__init__()
self.in_feature = in_feature
self.out_feature = out_feature
self.s = s
self.m = m
self.weight = Parameter(torch.Tensor(out_feature, in_feature))
nn.init.xavier_uniform_(self.weight)
self.easy_margin = easy_margin
self.cos_m = math.cos(m)
self.sin_m = math.sin(m)
# make the function cos(theta+m) monotonic decreasing while theta in [0°,180°]
self.th = math.cos(math.pi - m)
self.mm = math.sin(math.pi - m) * m
def forward(self, x, label):
# cos(theta)
cosine = F.linear(F.normalize(x), F.normalize(self.weight))
# cos(theta + m)
sine = torch.sqrt(1.0 - torch.pow(cosine, 2))
phi = cosine * self.cos_m - sine * self.sin_m
if self.easy_margin:
phi = torch.where(cosine > 0, phi, cosine)
else:
phi = torch.where((cosine - self.th) > 0, phi, cosine - self.mm)
one_hot = torch.zeros_like(cosine)
one_hot.scatter_(1, label.view(-1, 1), 1)
output = (one_hot * phi) + ((1.0 - one_hot) * cosine)
output = output * self.s
return output
결론 부터 말하면
arcface는 분류 문제를 학습할 때 사용(위 코드의 out_feature는 클래스 개수이다)되며,
분류 학습의 부산물로 클래스 간에는 확실한 분별력을, 클래스 내에선 응집력을 갖는 임베딩을 학습할 수 있다.
따라서, arcface를 이용해 사람 얼굴 이미지에 대한 의미 있는 표현(임베딩)을 얻고 싶다면
A, B, C ... Z class(인물명 혹은 아이디) 각각에 대해 여러 개의 이미지를 마련한 뒤
arcface와 softmax를 결합하여 분류 모델을 학습해야 한다.
학습한 뒤에 임베딩만 필요하다면, 분류 레이어는 떼어 내고 임베딩만 활용하면 되는 것이다.
ArcFace의 동작 방식
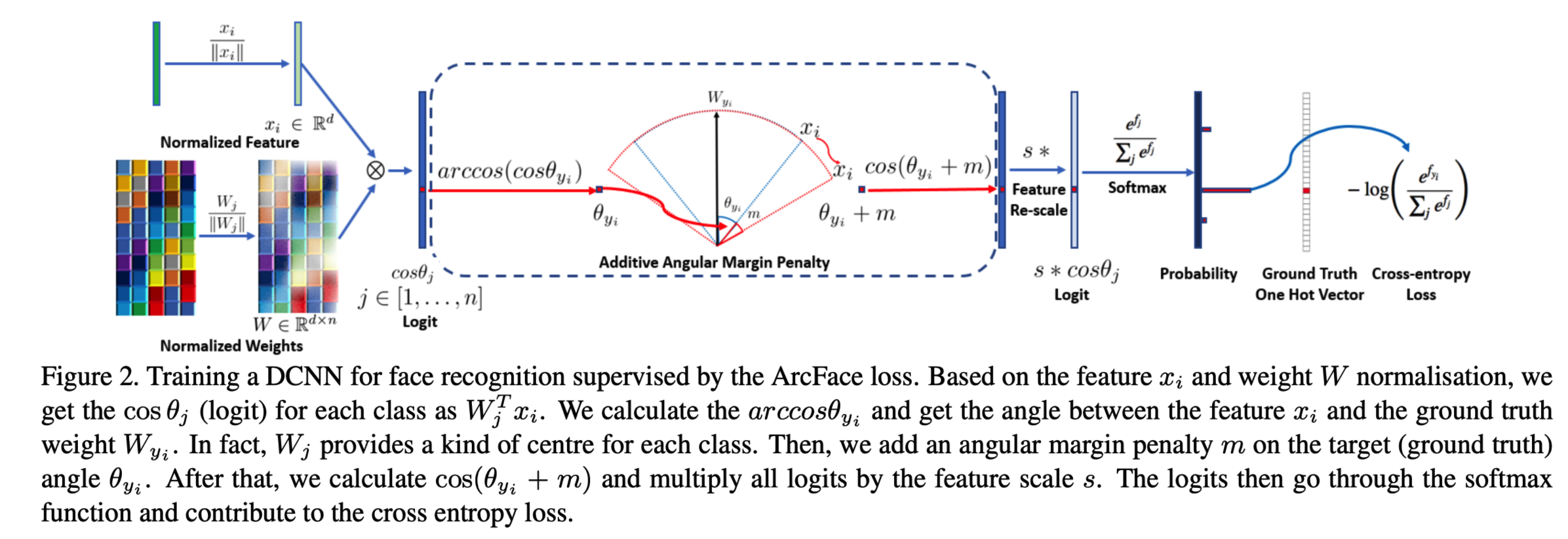
빠른 이해를 위해 다음 몇 가지를 이해하면 좋다.
(아래 것들을 놓치고 있어서 이해하는데 오래걸림)
- 특정 클래스를 의미하는 벡터들이 클래스 개수 만큼 있고, 입력이 들어왔을 때 얻어지는 벡터를 내적하여 각도를 구할 것임
- 정답 클래스와의 각도가 최소화 되도록 학습
- 분류 모델을 학습할 때, softmax를 거쳐 확률 분포로 바꾼 뒤 CrossEntropy와 결합 되어 학습 될 때
- 정답 위치에 해당하는 확률을 최대화 (1.0에 가깝게) 만들려고 한다.
- 여기서 중요한 것은 softmax에 들어가는 입력이 cosine(theta) 라는 것
- 각도(theta)가 0(정답과 예측이 완전히 일치) 될 수록 cosine 값은 커진다 (1에 가까워짐)
- 따라서 CrossEntropy가 정답 위치를 최대화 하는 과정에서
- 특정 입력의 임베딩이 정답 클래스 임베딩과 각도(theta)는 최소화 되도록 학습
- 여기서 중요한 것은 softmax에 들어가는 입력이 cosine(theta) 라는 것
- 정답 위치에 해당하는 확률을 최대화 (1.0에 가깝게) 만들려고 한다.
- theta에 m(margin)을 더하는 것의 의미
- 특정 입력을 넣었을 때 나오는 임베딩과의 정답 클래스 임베딩의 각도를 현재 계산된 것 보다 조금 더 멀게 설정
- 어차피 멀어진 각도는 CrossEntropy에 의해 최적화 될 때 최소화 됨
- 특정 입력을 넣었을 때 나오는 임베딩과의 정답 클래스 임베딩의 각도를 현재 계산된 것 보다 조금 더 멀게 설정
이제 논문에 나오는 그림(figure.2) 설명과 코드를 대조해가며 한줄 한줄 읽어보면 이해가 쉽게 갈 것이다.
- self.weight은 (입력 차원 x 클래스 개수)로 이루어진 메트릭스
- input과 self.weight을 각각 normalize 해줌으로써 길이 1인 구 위에 위치할 수 있게 함
- sine을 구하는 이유?
- 삼각함수의 덧셈 정리 cos(x + y) = cosx * cosy + sinx * siny
- cos(theta + m)을 구하기 위해서 미리 구해놔야함
- sine은 어떻게 구함?
- 피타고라스 공식을 이용하면 코사인 제곱 + 사인 제곱 = 1
- easy_margin은 뭐임?
- github.com/ronghuaiyang/arcface-pytorch/issues/2 참고
- the purpose of the easy margin is not to consider the theta + m > pi
- github.com/ronghuaiyang/arcface-pytorch/issues/2 참고
- 참고로 그림에 있는 arccos는 실제 구현 코드엔 등장할 필요가 없다. 왜 cos theta에 cosine의 역함수인 arccos를 적용시켜 theta로 역변환 할 필요가 없는지는 각자 직접 생각해보자.
참고자료
ArcFace: Additive Angular Margin Loss for Deep Face Recognition(2019) review
Face Recognition(얼굴 인식)분야에서 사용되는 Loss인 ArcFace loss에 대한 논문이다. 얼굴 인식 분야를 공부하는 것은 아니나, 다른 논문을 읽다가 loss function으로 ArcFace loss를 활용하는 논문이 있어 해당
cumulu-s.tistory.com
ArcFace: Additive Angular Margin Loss for Deep Face Recognition.
각도의 경우 rotaion-invariant, scale-invarint 속성이 보장된다.
norman3.github.io
Metric Learning 이란 - 학습 방법(Loss)
*크롬으로 보시는 걸 추천드립니다* 본 "Metric Learning 이란 - 학습 방법(Loss)"를 보시기 전에 1) Metric Learning 이란 - 기본 2) [논문요약] Deep Face Recognition : A Survey - ① 탄 순서로 먼저 보시..
kmhana.tistory.com
메트릭러닝 기반 안경 검색 서비스 개발기(2)
본 글은 AI 가상피팅 기반 안경쇼핑앱 ‘라운즈’에 최근 추가된 안경 검색 서비스 ‘Glass Finder’의 개발기를 공유하고자 작성된 글입니다. 지난 1부에서는 메트릭 러닝 기반 안경 검색 프로젝트
blog.est.ai
'DL&ML > concept' 카테고리의 다른 글
| ML General 잡질문/답변 (기술면접) (3) | 2021.05.14 |
|---|---|
| ReLU가 Non-linear인 이유? (0) | 2021.04.14 |
| Seq2Seq & Beam Search (0) | 2021.04.14 |
| Classification에서 CrossEntropy를 Loss 함수로 쓰는 이유? (0) | 2021.04.13 |
| Posterior, Likelihood, Prior (0) | 2021.04.12 |