Posterior, Likelihood, Prior

베이즈 정리를 구성하는

Posterior, Likelihood, Prior가 헷갈리는 이유는

각각을 구분하는 기준을 아직 모르기 때문이다.

 

 

https://seeve.medium.com/machine-learning-bayes-theorem-2f48c33d51e5

 

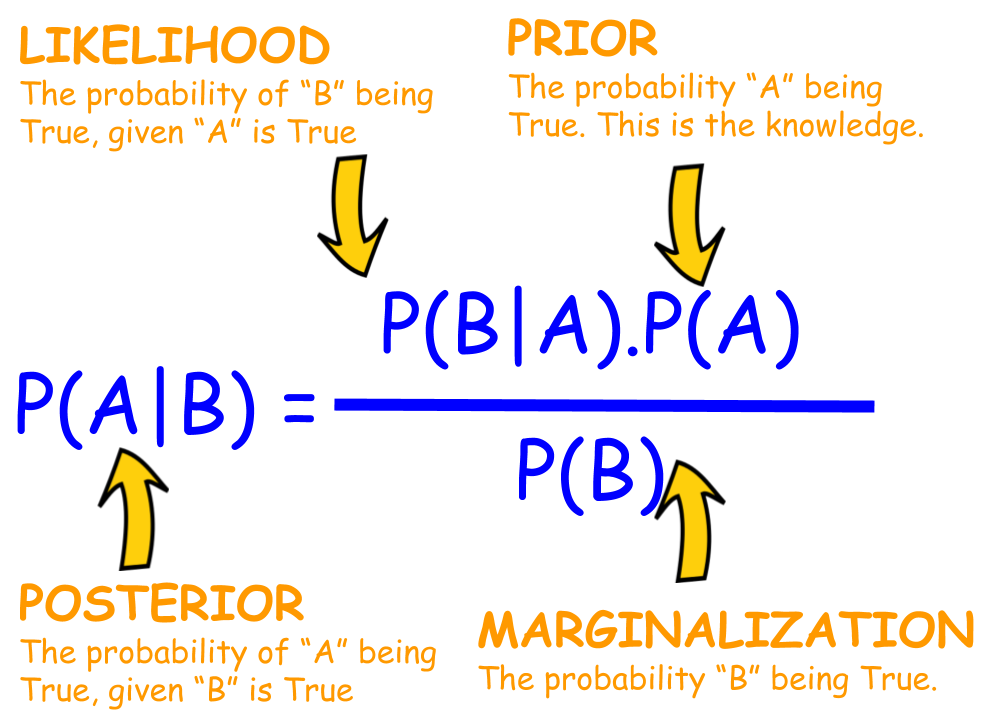
우선 셋을 구분하기 위해선

 

문제 해결을 위해

구하고자 하는 대상,

주어진 대상(관측 값)이 뭔지 알아야 한다.

 

즉, 구하는 대상, 주어진 대상이 바뀌면 저 셋도 바뀌게 된다.

 

Posterior

관측 값이 주어졌을 때, 구하고자 하는 대상이 나올 확률

Likelihood

구하고자 하는 대상이 정해졌다고 가정할 때, 주어진 대상이 나올 확률

Prior

구하고자 하는 대상 자체에 대한 확률

 

예를 들어,

주어진 대상 = 학습 데이터이고

구하는 대상 = 모델 파라미터면

 

Posterior = P(w|D)

Likelihood = P(D|w)

Prior = P(w)

 

인 것이다.

 

MLE는 P(D|w)를 최대화 하는 w를 찾는 방법이다.

 

또 다른 예시로,

신발 사이즈를 보고 남자/여자를 맞출 때

 

주어진 대상 = 신발 사이즈

구하고자 하는 대상 = 남/여 클래스

 

Posterior = P(성별|신발사이즈)

Likelihood = P(신발사이즈|성별)

Prior = P(성별) = P(남자) or P(여자)

 

이 문제를 풀기 위해 Likelihood만 보고 판단할 수도 있지만,

Prior에 대한 사전 지식이 있다면 좀 더 엄밀히 문제에 접근할 수가 있다.

 

보통은 Prior를 구하는 것이 쉽지 않기 때문에

균등분포라고 가정하고 MAP가 아닌 MLE로 접근한다.

 

 

참고자료!!

Bayes Theorem과 Sigmoid와 Softmax사이의 관계

Cross Entropy의 정확한 확률적 의미