Regression에서 MSE를 Loss 함수로 쓰는 이유?

이전에 아래 글에서 Likelihood & MLE에 대한 정리를 했었는데,

분류 문제에 대한 설명은 되지만,

리그레션 문제에 대한 설명을 하려 할 때 감이 잘 오지 않는다.

Likelihood & MLE(최대 우도 추정) 1

이번엔 Regression에서 MSE를 Loss 함수로 쓰는 이유를 정리하려 한다.

(결론 부터 말하면, 리그레션 모델의 출력을 가우시안 분포의 평균 값으로 가정하고 MLE를 했을 때, Likelihood를 의미하는 식이 미분을 통해 결국 MSE로 바뀌게 된다)

 

딥러닝은 단순 함수의 파라미터를 모사하는 것이기도 하지만,

결국 '확률 분포'를 모사하는 것으로 해석이 가능하다고 들었다.

 

분류 문제는 멀티노미얼 분포를 모사하는 것으로 자연스레 이해가 된다.

(네트워크 자체의 출력이 softmax를 거쳐 확률 분포로 나오니까...)

따라서 두 확률 분포(정답, 예측)를 비슷하게 만들기 위해 NLL 혹은 CrossEntropy를 최소화 했었다.

 

그런데, 리그레션은 문제는 어떤 분포를 모사하는 것일까?

 

결론 부터 말하면,

가우시안 분포를 모사하는 것이다.

 

그런데 뉴럴넷이 분류 문제에서 처럼 분포 자체를 출력(softmax)하는 것이 아니라

가우시안 분포의 평균(뮤) 값을 출력한다고 이해해야 한다.

 

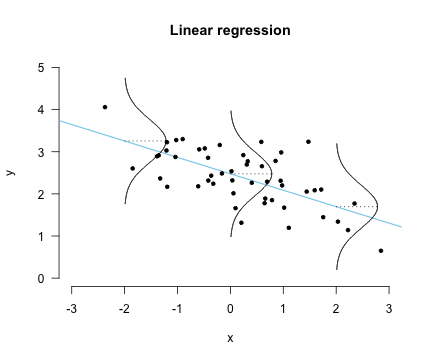
리니어 모델을 기준으로 특정 입력 값을 모델에 넣었을 때 나오는 출력 값이 단순한 값이 아닌

어떤 가우시안 분포가 있고 그 분포의 평균 값이라고 생각하자는 것!

(이렇게 이해하는게 더 자연스러울 수 있다. 모델의 예측 값은 4이지만

실제 세상에선 그 주변으로 불확실성을 가질 수 있기 때문이다)

https://www.r-bloggers.com/2019/01/curve-fitting-and-the-gaussian-distribution/

MLE 복습

어떤 데이터셋 D = {(x_i, t_i)} 가 주어져 있을 때

우리는 데이터셋을 잘 설명하는 뉴럴넷의 파라미터를 구하기 위해서

argmax sum{log p(t_i | x_i ; Θ)}, i: 0 ~ N

를 통해 log likelihood를 최대화 함으로써 파라미터를 구했다.

(- 를 붙이면 NLL이 되어 최소화 문제로 바뀌었고)

 

Gaussian Distribution + MLE = Regression Loss

리그레션 문제를 MLE로 풀 때

우리는 Likelihood 값인 p(t_i | x_i) 을 얻기 위해 가우시안 분포를 가정한다.

 

결론적으로, 주어진 데이터 셋의 x_i는 뮤(μ)를 정하는데 기여한다.

뉴럴넷의 입력으로 x_i가 들어가면 출력 값으로 뮤(μ)가 나오는 것을 가정하기 때문이다.

 

헷갈릴 여지가 있어 설명을 더하면,

아래 PDF식에서 x가 정답 t_i를 의미하며

x_i에 의해 뮤(μ)가 정해졌을 때 t_i를 PDF수식에 넣으면 (x=t_i)

해당 가우시안 PDF에서 Likelihood를 얻을 수 있다.

 

수식 1

앞서 언급 한 것 처럼, 위 수식 상에서

- 뮤(μ)는 네트워크의 예측 값,

- x는 Ground Truth(t) 값으로 생각해야 한다.

문제를 간단하게 하기 위해 시그마는 그냥 상수로 주어진다고 가정.

확신의 정도에 따라 시그마는 달라지게 된다.

 

아래 식은 형민님 블로그에서 가져온 수식인데,

t ~ N ( ) 부분은 네트워크에서 출력 된 값을 평균으로 생각하는 Normal 분포에서

정답 t를 샘플링 했다는 의미고,

 

p(t|x)는

x를 넣으면 출력되는 뮤(μ)에 의해 가우시안 분포가 정해질 때,

t가 나올 likelihood를 정의 한다.

 

w는 우리의 현재 뉴럴넷 파라미터를 의미하고,

y(x|w)의 의미는, w가 주어졌을 때 x를 뉴럴넷에 넣음으로써

나오는 출력값(뮤 ; μ)을 의미한다.

 

수식 2 https://hyeongminlee.github.io/post/bnn002_mle_map

 

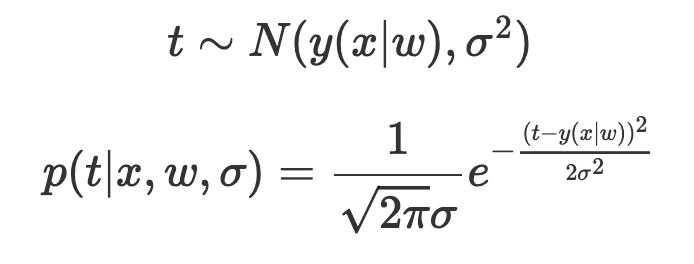
이 때 주어진 데이터를 통해 얻을 수 있는 likelihood를 최대화 할 수 있도록 학습하면

뉴럴넷은 입력 값 x에 적절히 대응하는 가우시안 분포의 평균 값을 예측하도록 학습이 된다.

 

주어진 데이터 셋 (N개)에 대한 Likelihood를 정의할 수 있고

(데이터셋의 example 끼리는 모두 독립이기 때문에 곱의 법칙으로 표현 가능)

 

수식 3 https://hyeongminlee.github.io/post/bnn002_mle_map

 

이 때, gaussian PDF에 로그를 취한 상태에서 w에 대해서 편미분을 하면 어떻게 될까?

w와 상관 없는 텀을 모두 날려 정리하고, 최소화 문제로 변형하기 위해 앞에 -를 곱해주면

아래와 같은 MSE와 동일한 수식이 나오게 된다.

 

수식 4 https://hyeongminlee.github.io/post/bnn002_mle_map

 

따라서 리그레션 문제를 푸는 것은

뉴럴넷이 가우시안 분포의 평균 값을 예측한다고 가정할 때,

MSE를 이용하여 가우시안 확률 분포를 모사하는 것으로 해석이 가능하게 된다.

 

참고 자료 (필독! 정말 좋은 자료)

Maximum Likelihood Estimation(MLE) & Maximum A Posterior(MAP) | Hyeongmin Lee's Website